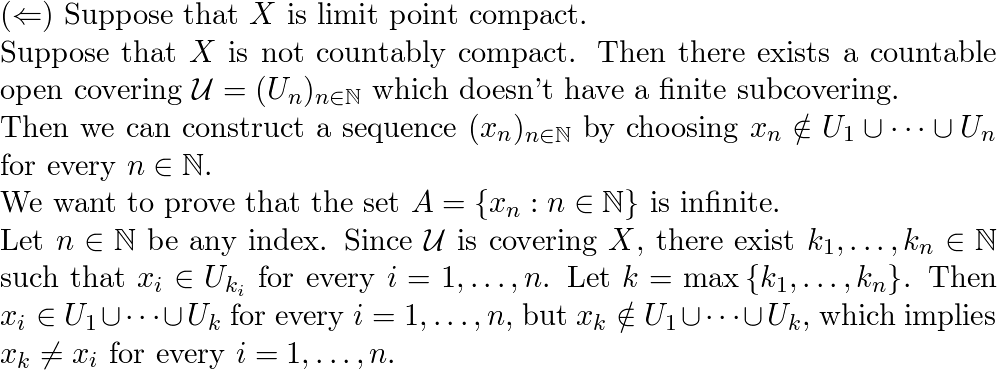general topology - A sequentially compact space is countably compact. - Mathematics Stack Exchange
25. On Pseudo,compact and Countably Compact Spaces
SOLVED: 9. Countable Compactness: A metric space in which every open cover has a countable subcover is sometimes called a countably compact space. Countable compactness is not as strong a condition as
PDF) First countable, countably compact, noncompact spaces | Peter Nyikos - Academia.edu
X be sequentially compact then X be countably compact / compactness in topology / L 10/ topology MSC - YouTube
Every Countably compact metric space has BWP | Compactness | Real Analysis - YouTube
PDF) Various countably-compact-ifications and their applications | Akio Kato - Academia.edu
SOLVED: Let X be a countably compact space. a) Let f: X â†' Y be a continuous and surjective function, where Y is a topological space. Show that Y is countably compact.
Countably compact metric space 2nd countable - Corollaries - YouTube
A space X is said to be countably compact if every countable | Quizlet
PDF) First countable, countably compact, noncompact spaces | Peter Nyikos - Academia.edu
Countably Compact set | Locally Compact set | Examples | Set Topology || Lecture 44 - YouTube
SOLVED: Q4: a) Define compact, sequentially compact, and countably compact. Discuss the compactness and sequential compactness of the following subspaces of R2. 1) (x, 25/211 < x < 2 2) (x, sin(x-15)/1 <
Compact space - Wikipedia
Show that X is countably compact if and only if every nested | Quizlet
A space X is said to be countably compact if every countable | Quizlet
Solved 1. A countably compact space is a topological space | Chegg.com
general topology - Subspace of regular countably compact $X$ consisting of all points at which $X$ is weakly countably tight is $G_\delta$ - Mathematics Stack Exchange
compactness - Why every countably compact space is $s-$ separated? - Mathematics Stack Exchange
A COUNTABLY COMPACT SPACE AND ITS PRODUCTS1 theorem of Frolik [4, Theorem 3.5].
general topology - A metric space is compact iff it is pseudocompact - Mathematics Stack Exchange
Axioms | Free Full-Text | Weakly and Nearly Countably Compactness in Generalized Topology
