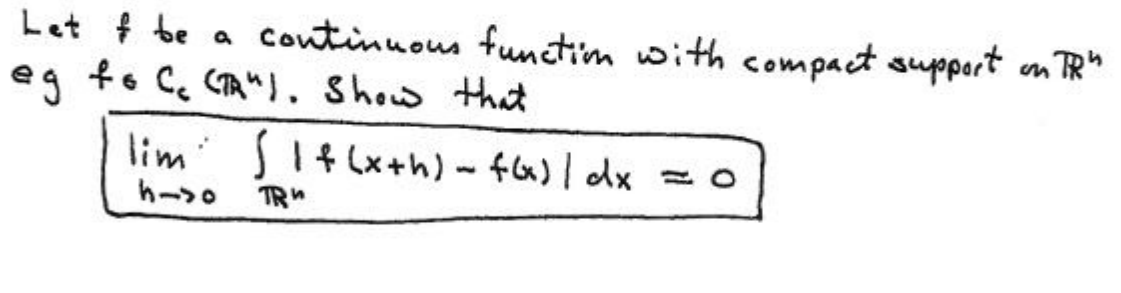Bump function - Wikipedia
Analysis WebNotes: Chapter 06, Class 31
More on the multivariate Helly theorem
Solved Problem 4 (test functions) Let Cc0(R) denote the | Chegg.com
Introduction to Variational Methods and Applications - ppt download
Bump function - Wikipedia
analysis - Compact support functions dense in $L_1$ - Mathematics Stack Exchange
real analysis - Rudin's RCA Theorem $3.17$ - Mathematics Stack Exchange
Lecture 11 (Part 3): Proof that space of continuous functions with compact support is not complete - YouTube
Equivalence definition of continuous operator between test function space: an exercise from Dyatlov lecture notes on differential analysis - Mathematics Stack Exchange
Solved which have a compact support in N. We start by | Chegg.com
Solved Let K be a compact and V be a bounded open in RN such | Chegg.com
Functional analysis in mechanics 2e | PDF
Solved Let of be a continuous function with compact support | Chegg.com
PDF) Continuous functions with compact support
Compact Support -- from Wolfram MathWorld
real analysis - How does partition of unity imply that for a compact $D$, there is only finitely many $ \operatorname{Support}\phi_i$ that intersect with $D$? - Mathematics Stack Exchange
Math 202B Solutions
harmonic analysis - Compactly supported continuous functions as a Tomita algebra - MathOverflow
analysis - If $X$ is compact and Hausdorff space, then vanishing at infinity implies compact support - Mathematics Stack Exchange
Solved Let f be a continuous function with compact support | Chegg.com
Lecture 11 (Part 3): Proof that space of continuous functions with compact support is not complete - YouTube
SOLVED: Please show me all the steps clearly with an explanation to solve, and write all the details. This problem is in Partial Differential Equation. Can you please use clear handwriting because
